日志
尧代观象台的相关计算
热度 3 ||
昨天看了一个考古节目,说在距今4700年的山西省襄汾县陶寺城遗址发现一个观象台。在当地发掘中发现一处夯土台上有若干柱子的基础,考古人员把相关数据交给中国天文学者进行计算,认为这是一个古观象台。从一个固定观测点看,在不同的节气日,太阳升起时出现在不同的柱子缝隙之间。《史记-五帝本纪》记载尧帝【其仁如天,其知如神...乃命羲、和,敬顺昊天,数法日月星辰,敬授民时。】因此,考古人员大胆推断这个遗址可能正是帝尧的都城。(下图来自网络)


节目中提到,为了计算太阳升起时的角度,很费了一番周折。开始竟然是等到冬至去实测,结果天气不作美。看到这,我想起了这篇《日夜的方程》中计算日出、日落时间的方程。稍加改变,就可以计算日出时太阳的角度了 -- 也就是阳光与地面正南方向的角度。如果地球自转轴没有倾斜而是与公转轨道平面垂直,那么太阳总是在正东方向升起,与正南方向夹角为90度。现在我们需要计算的是实际情况。为完整起见,我下面重复《日夜的方程》的部分内容。
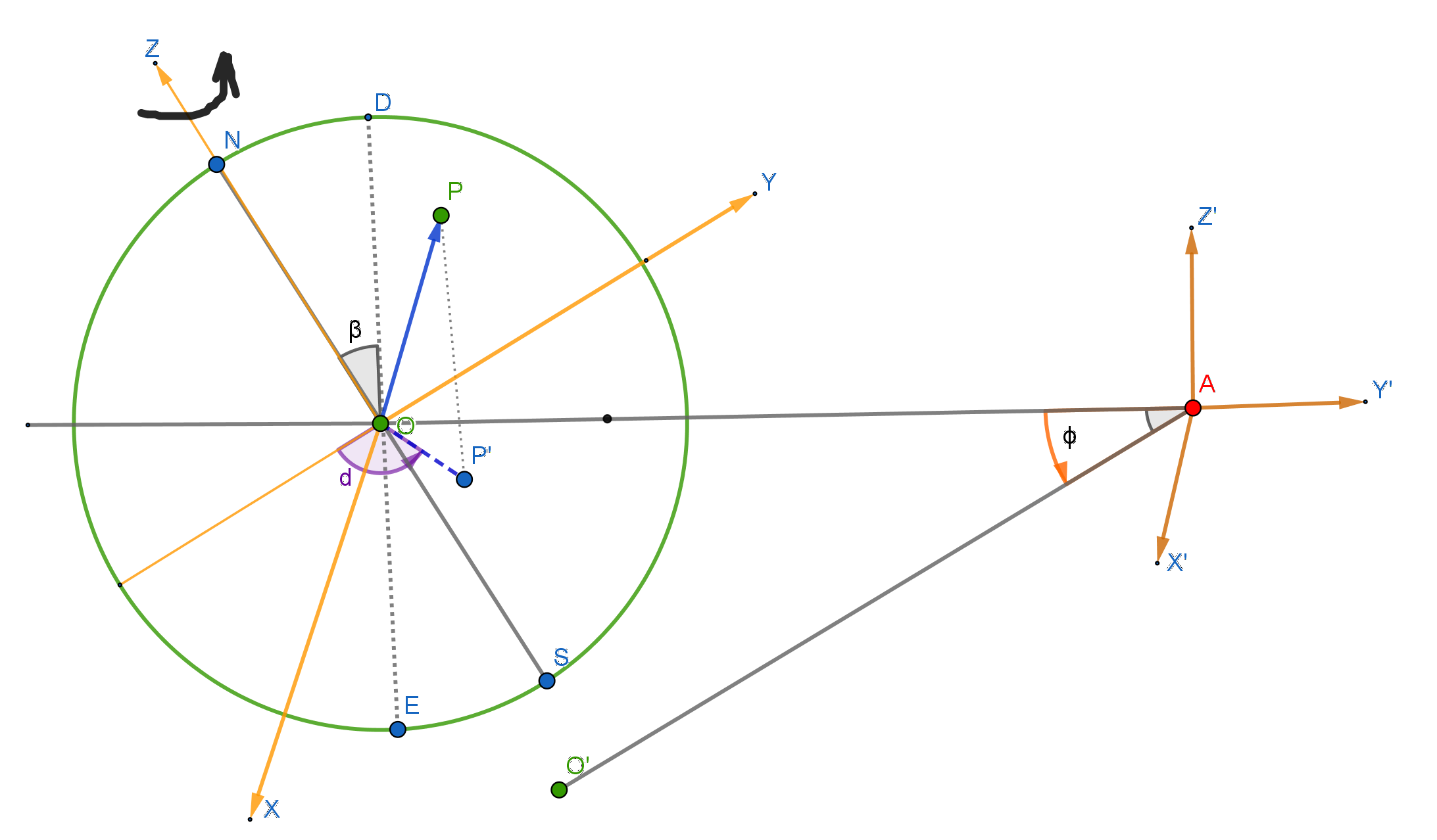
要做这个计算,需要先确定坐标。那么就让我们以冬至这点的状态设置坐标,然后开始计算。下图中,O是地球的球心,N是北极,S为南极,地球绕 NS 轴自转,P为地球表面一点; A 为太阳所在,但应该想象太阳在右边无限远处,阳光是平行的,方向是从A到地心的连线;地球绕太阳的轨道是在水平面上,DOE 线垂直于轨道平面;地球自转轴与 DOE 线的夹角为 β,就像个倾斜的陀螺。冬至日的时候,NOAD 四点在同一个面上,垂直于地球轨道平面。此时,地球自转轴与阳光的夹角 <NOA 就是地球自转倾角 β 加上90度。计算 OP 与阳光 的角度 θ 是一个相当直接的几何问题。坐标设置如下图中的 XYZ 与 X'Y'Z'。

上图中,设P点的纬度为 L,P在XY平面上的投影为 P', OP' 与 -Y 轴角度为 d 。考虑地球在自转的同时还在公转。我们希望得到的是一个含时间的方程,同时考虑自转与公转。在XYZ坐标系中,OP的方向为 (cosLsind,−cosLcosd,sinL)。而在X'Y'Z'坐标系中,AO'方向为 (sinϕ,−cosϕ,0)。要计算两者的角度需要找出两个坐标之间变换关系。这是一个角度为 β的转动。我们有
ˆx=^x′ˆy=cosβ ^y′+sinβ ^z′ˆz=−sinβ ^y′+cosβ ^z′
代入计算OP 与 O'A 之间的角度,也就是阳光与垂直于地面的标杆的角度,我们得到
cosθ=[cosd cosLcosβ+sinLsinβ]cosϕ+sinϕsindcosL
现在我们计算阳光与地面正南方向的夹角α。XYZ 坐标中P处正南方向为 (sinLsind,−sinLcosd,−cosL)。进行坐标变换之后计算与阳光方向的余弦 ,我们得到
cosα=[cosβsinLcosd−sinβcosL]cosϕ+cosLsindsinϕ
太阳升起、落下的时候,阳光与垂直标杆垂直,因此 cosθ=0。所以,日出、日落时
[cosd cosLcosβ+sinLsinβ]cosϕ+sinϕsindcosL=0
设地球自转角速度为 ω, 公转角速度为 Ω, t 为时间,则 d=ω t, ϕ=Ω t。
因此太阳与直立标尺的角度 θ 的方程为
cosθ=[sinLsinβ+cosLcosβ cos(ω t)] cos(Ω t)+cosLsin(ω t)sin(Ω t)
至此,我们得到计算日出、日落时间的方程是:
[sinLsinβ+cosLcosβ cos(ω t)] cos(Ω t)+cosLsin(ω t)sin(Ω t)=0
或者:
sinLsinβ+cosLcosβ cos(ω t)cosLsin(ω t)=−tanΩt
从上面的方程计算出日出时间,并代入阳光与正南方向夹角的公式
cosα=[cosβsinLcos(ωt)−sinβcosL]cos(Ωt)+cosLsin(ωt)sin(Ωt)
即可算出太阳升起时阳光的角度。代入实际数据,倾角 \beta = 23.44 度,计算出冬至日北京(纬度取北纬40度)太阳升起阳光与正南方向的角度为121.27 度。夏至日太阳升起时角度 为58.7度。如果考虑折射,这个角度将略有不同。另外,地球自转倾角以两万六千年为周期变化,因此4700年前倾角与现在也有不可忽略的差异。
附:Python 代码
# -*- coding: utf-8 -*-
"""
Created on Fri Jul 8 21:00:50 2018
@author: YDX
"""
from sympy import symbols, cos, sin, acos, sqrt, pprint,diff,solve,nsolve, Eq, latex, integrate,pi, simplify, Matrix
from sympy.plotting import plot
import matplotlib.pyplot as plt
import numpy as np
import sympy as sym
# alpha -- angle between sun ray and tilt axis
# tilt -- titl axis
# phis -- angle around sun
tilt, phis, d, lat, sp, t = symbols(' tilt phis d lat sp t')
# z^ = cos(tilt) z'^ - sin(tilt) y'^
# y^ = sin(tilt) z'^ + cos(tilt) y'^
# x^ = x'^
# sun ray: [sin(phis) x'^, - cos(phis) y'^,0]
#point: [cos(lat)*cos(d), cos(lat)*sin(d), sin(lat)]
m = sym.zeros(3,3)
m[0,0]=1
m[1,2] = sin(tilt)
m[1,1] = cos(tilt)
m[2,1]= -sin(tilt)
m[2,2]= cos(tilt)
print(m)
loc = Matrix([cos(lat)*sin(d), -cos(lat)*cos(d), sin(lat)])
east = -loc.cross(Matrix([0,0,1]))
tnorth=-Matrix([-sin(lat)*sin(d), sin(lat)*cos(d), cos(lat)])
print ("east", east)
east_len = simplify(sqrt((sym.Transpose(east)*east)[0,0]))
print (east_len)
east = east/east_len
print ("east norm", east)
east2 = simplify( loc.cross(tnorth))
print ("east 2", east2)
north = Matrix([0,0,1])
ray = Matrix([sin(phis), - cos(phis),0])
loc_sun = sym.Transpose(m) * loc
east_sun = sym.Transpose(m) * east2
tnorth_sun = sym.Transpose(m) * tnorth
dotp = sym.Transpose(ray)*loc_sun
dotn = sym.Transpose(ray)*tnorth_sun
dote = sym.Transpose(ray)*east_sun
#print(dotp.shape, dotp)
dot=simplify(dotp[0,0])
print("dotn=",dotn)
dotn=simplify(dotn[0,0])
print("dotn=",dotn)
sp = acos(dot)
print("angle", sp)
sp2= acos(dotn)
print(latex(sp))
dlen= 23+56/60+4/3600
ylen = 365.2422
oe = 2*np.pi * 24/dlen
os = 2*np.pi/ylen
d2rad = np.pi/180
til = 23.43688*d2rad
lati = 40*d2rad
def angle(t, tilt, lat):
d = oe *t
phis = os *t
return np.arccos((np.cos(d)*np.cos(lat)*np.cos(tilt) + np.sin(lat)*np.sin(tilt))*np.cos(phis) + np.sin(phis)*np.sin(d)*np.cos(lat))
ts=np.arange(0,365,0.005)
angles = angle(ts, til, lati)
plt.plot(ts[angles>np.pi/2], angles[angles>np.pi/2])
spd =sp.subs({lat:lati, tilt:til, phis:os*t, d:oe*t})
sp2d =sp2.subs({lat:lati, tilt:til, phis:os*t, d:oe*t})
print(latex(spd))
sols=[]
morning_angles=[];
day=0
lasts=0
intv = 0.2
a1 = np.arccos(-np.tan(til)*np.tan(lati))
d1=nsolve(Eq(spd,np.pi/2), t, 0)
d2=nsolve(Eq(spd,np.pi/2), t, d1+0.4)
d1=nsolve(Eq(spd,np.pi/2), t, 0)
d3=nsolve(Eq(spd,np.pi/2), t, 1)
print (d1,d2,d3, d1*24, d2*24, (d2-d1)*24, (d3-d1)*24)
d5= d1*oe
print ("diff=", a1, a1/d2rad, d5, (d5-a1)*24*60/oe)
lasts=0
#lasts = nsolve(Eq(spd,np.pi/2), t, [lasts+0.01,lasts+intv], solver='bisect')
#print (lasts)
#raise SystemExit
while lasts<185:
try:
lasts = nsolve(Eq(spd,np.pi/2), t, [lasts+0.0001,lasts+intv], solver='bisect')
sols.append(lasts)
ma = sp2d.subs({t:lasts}) /d2rad
sols.append(ma)
intv = 0.4
#print ("Found " +str(lasts))
except:
#print ("no solution", lasts, lasts+intv)
lasts = lasts+intv
days = np.array(sols)
sz = days.size
if(sz%4):
sz = sz- sz%4
nd=np.reshape(days[0:sz], (-1,4))
print(nd)







